【頭の体操】円錐（えんすい）の表面積は習った事の応用#13

＜円錐（えんすい）の表面積は習った事の応用問題です＞

直円錐（ちょくえんすい）

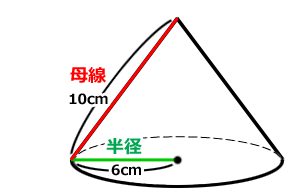
直円錐とは、底面の円の中心と頂点とを結ぶ線が、底面に垂直である円錐のことです。

図のような母線10cm、半径6cmの直円錐があるとします。

この直円錐の表面積はいくらでしょう？

直円錐を分解

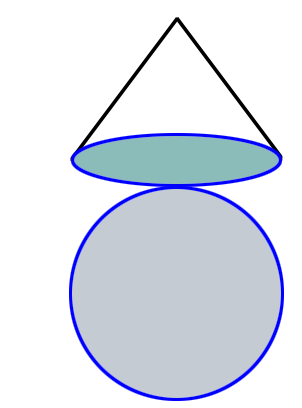
直円錐の底面を外してみました。

上部の円錐部分と、底面の円に分けることができます。

上部の円錐部分を展開したら、どんな形になるでしょう。

直円錐の展開図

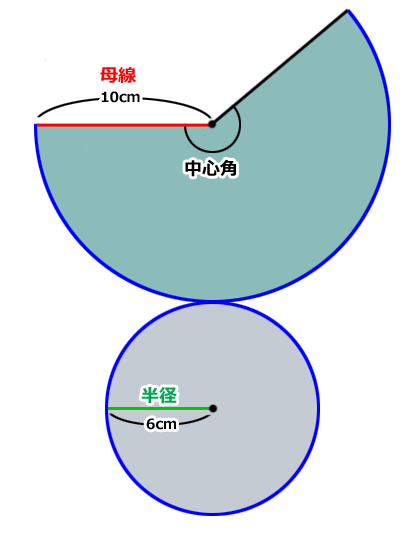
こちらが展開図です。上部は扇形になります。

母線は扇形の半径となります。

中心角の求め方です。

扇形の弧の部分と、底面の円の円周は同じ寸法です。

（扇形の青い部分と、底面の青い円周は同じ寸法です。）

母線×2×3.14×(中心角÷360)＝半径×2×3.14
　　　　　▼
母線×(中心角÷360)＝半径
　　　　　▼
母線×中心角÷360＝半径
　　　　　▼
中心角÷360＝半径÷母線
　　　　　▼
中心角＝半径÷母線×360

扇形の中心角は、6÷10×360＝216°です。

扇形の弧の長さは、母線×2×3.14×(中心角÷360)です。

円弧の長さ＝母線×2×3.14×(中心角÷360)
　　　　　▼
円弧の長さ＝母線×2×3.14×(半径÷母線×360÷360)
　　　　　▼
円弧の長さ＝母線×2×3.14×(半径÷母線)

扇形の円弧の長さは、10×2×3.14×(6÷10)＝37.68cmです。

底面の円周は、6×2×3.14＝37.68cmで、円弧の長さと同じになります。

直円錐の表面積

円の面積は、半径×半径×3.14で求められます。

扇形の面積は、母線×母線×3.14×(中心角÷360)です。

扇形の面積は、10×10×3.14×(216÷360)＝188.4c㎡です。

底面の面積は、6×6×3.14＝113.04c㎡です。

よってこの直円錐の表面積は、188.4＋113.04＝301.44c㎡です。

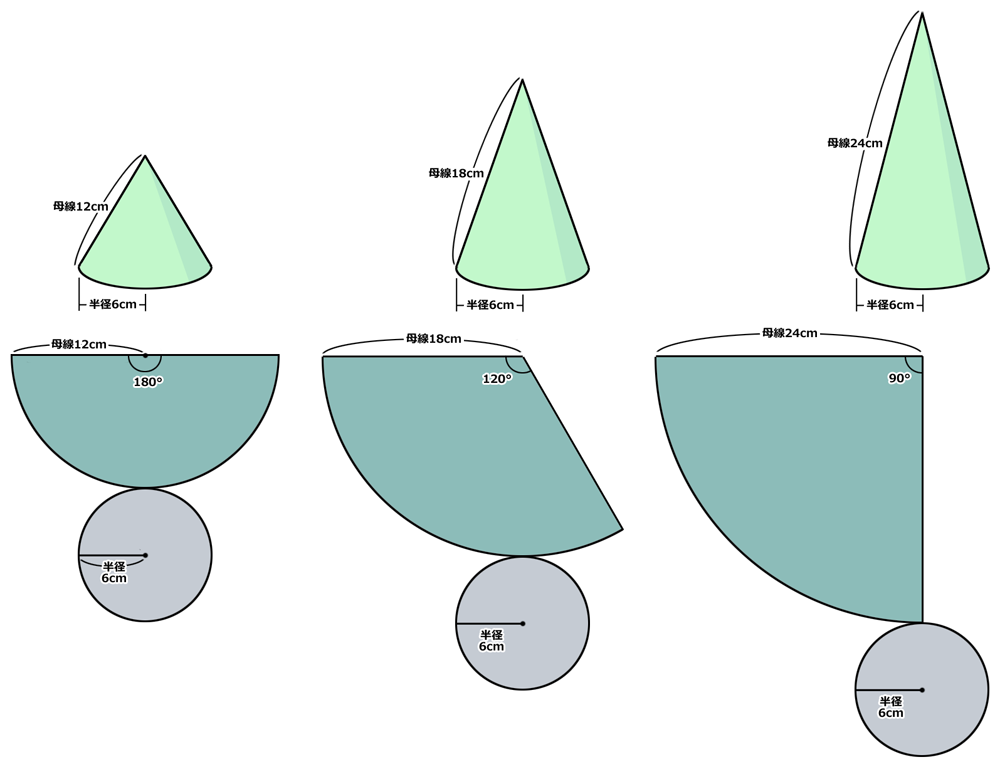
直円錐の母線を変えてみた

母線を変えると、このように展開図が変わってきます。

底面の半径6cmの円周は、6×2×3.14＝37.68cmです。

扇形の円弧の長さです。

円弧の長さ＝母線×2×3.14×(半径÷母線)

母線12cmの場合、12×2×3.14×(6÷12)＝37.68cmです。

母線18cmの場合、18×2×3.14×(6÷18)＝37.68cmです。

母線24cmの場合、24×2×3.14×(6÷24)＝37.68cmです。

円錐の母線を変更しても、展開した場合の円弧の寸法は変わりません。

展開図が頭の中でうまくイメージできなかったので、違うサイズの直円錐を描いてみました。