<頭が固い人には解けない問題?>
線を消す?
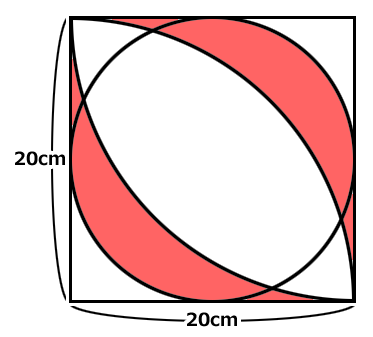
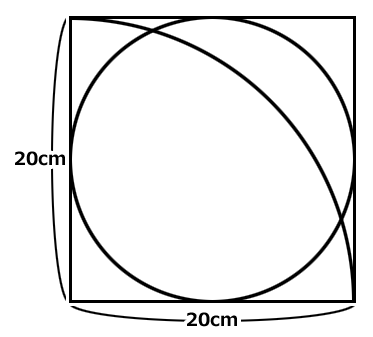
図のような正方形があります。正方形の一辺は20cmです。
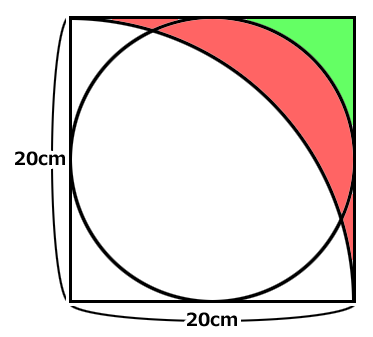
赤い部分の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
赤い部分の面積

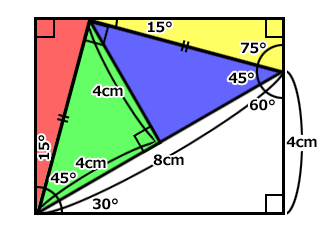
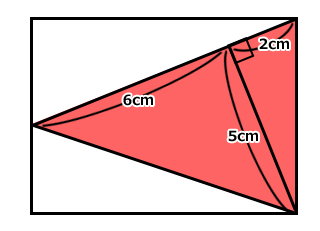
図のような長方形があります。
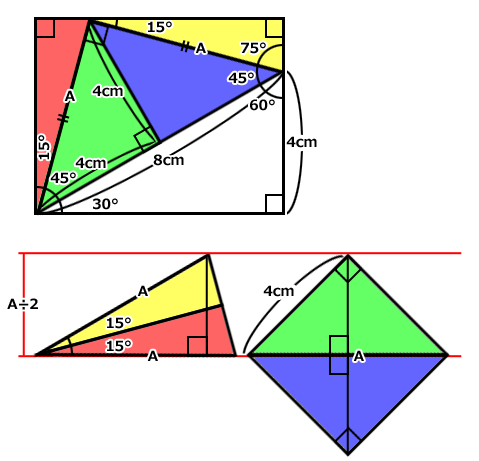
赤い部分の中に、直角二等辺三角形が一つと、直角三角形が二つあります。
赤い部分の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
長方形の面積は?
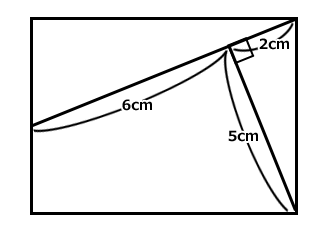
図のような長方形があります。
右上の角から左下へ直線が伸びています。
右下の角からその線に垂線が伸びています。
他の箇所の角度や寸法は不明です。
さて長方形の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
もっと見る?
-

-
【まとめ】頭の体操★頭の固い人には溶けないかも!
解けそうで解けない問題を集めてみました。頭の良さより柔らかさが必要です。