<頭が固い人には解けない問題?>
円が4つ接する図形
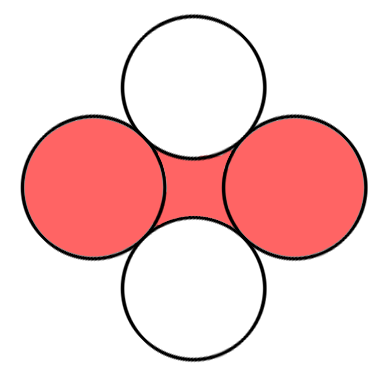
図のような半径10cmの円が4つあります。
4つの円はそれぞれ90°横方向の円と接しています。
さて、この図の赤い部分の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
+ 解答はここをクリック

図の中央に「✕」状の補助線を二本引いてみます。
2本の補助線は、それぞれの円の接線になっています。
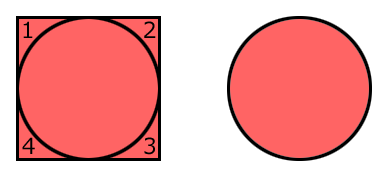
接線により出来た4つの図形を、左の円の周りに90°ごとにくっつけてみました。
円の半径は10cmですので、一辺20cmの正方形が出来上がりました。
赤い部分はこの正方形と、円1個となります。
よって、赤い部分の面積は、20cm×20cm+10cm×10cm×3.14=714c㎡になります。
高さが分からない図形
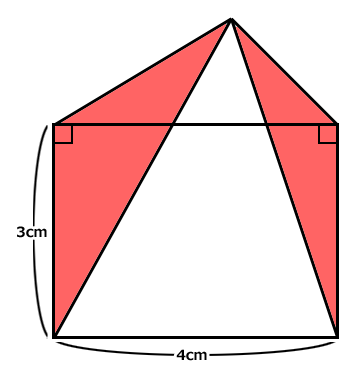
3cm×4cmの長方形の上に、底辺が4cmの三角形が乗っています。
三角形の頂点から、長方形の下の二つの角に線が伸びています。
上に乗っている三角形の高さは分かりません。
赤い部分の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
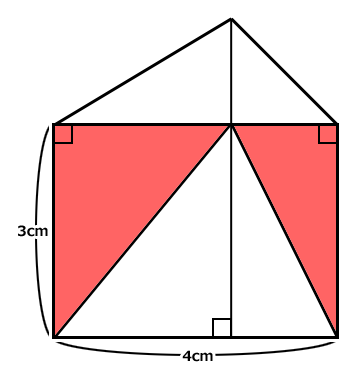
上に乗っている三角形の頂点から、長方形の底辺に向かって、垂線を降ろします。
その垂線に沿って、赤い三角形を長方形の中に、変形させながら移動します。
3cmを底辺として高さは変わらないので、面積は変わりません。
図のように移動させると、赤い部分は長方形の半分になります。
よって、赤い部分の面積は、3cm×4cm÷2=6c㎡になります。
正方形と正三角形
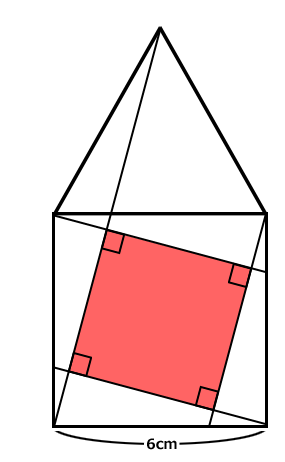
一辺6cmの正方形の上に、一辺6cmの正三角形が乗っています。
正三角形の頂点から、正方形の左下角に線を引きます。
その線と平行に1本、直角に交わる線を2本引きます。
それぞれの線の片方がが正方形の角に来るようにします。
中央に斜めになった赤い正方形が出来ます。
さて赤い正方形の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
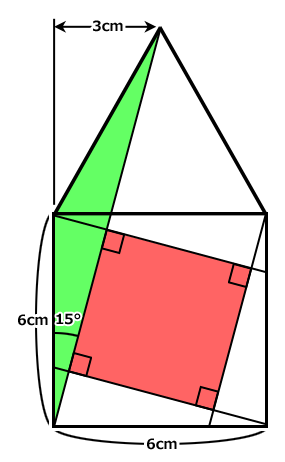
緑の部分は、二辺が6cmの平べったい二等辺三角形です。
二等辺三角形の頂点の角度は90°+60°で150°になり、残り二つの角度は15°になります。
正三角形を二等分すると、半分にした部分の一辺は6cmの半分の3cmになります。
緑の部分は、底辺6cm、高さ3cmの三角形でもあります。
緑の部分の面積は、6cm×3cm÷2=9c㎡になります。
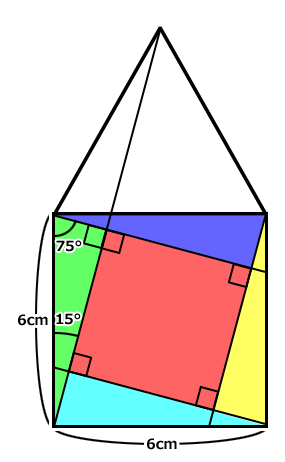
緑の二等辺三角形を半分にしました。面積は9c㎡÷2=4.5c㎡です。
緑の部分は斜辺が6cm、角度が15°、75°、90°の直角三角形です。
緑の三角形と、青、黄色、水色の三角形も、斜辺の長さと三つの角度が同じです。
よって、面積も同じになります。
緑、青、黄色、水色のそれぞれの直角三角形の面積は、4.5c㎡です。
一辺6cmの正方形から4つの直角三角形を引くと、赤い正方形の面積が求められます。
よって、赤い正方形の面積は、6cm×6cm-4.5c㎡×4=18c㎡になります。
もっと見る?
-

-
【まとめ】頭の体操★頭の固い人には溶けないかも!
解けそうで解けない問題を集めてみました。頭の良さより柔らかさが必要です。