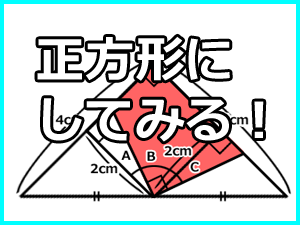
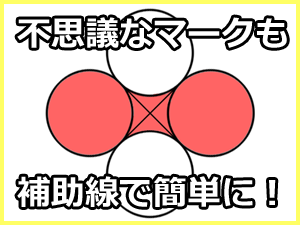
＜頭が固い人には解けない問題？＞
パックマンに見える面積
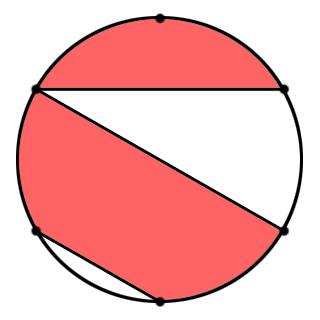
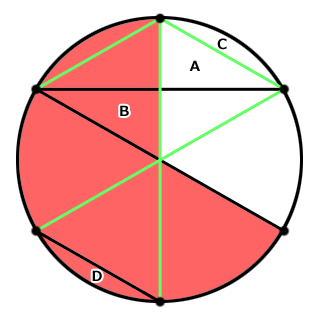
図のような半径3cmの円があります。
円周上には円周を六等分した六個の点があります。
この赤い部分の面積はいくらでしょう？
しばらく考えてください。分かりましたか？
＋ 解答はここをクリック
説明します。
図のように緑の補助線を引いてみます。
六等分された六個の点を結んでいるので、正三角形が見えてきます。
AとB、CとDは同じ面積です。
赤いAをBに、赤いCをDに移動します。
赤い部分は、円全体の4/6になりました。
よって赤い部分の面積は、3cm×3cm×3.14÷6×4＝18.84c㎡になります。
ずれた円の面積
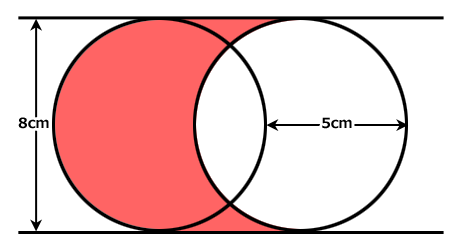
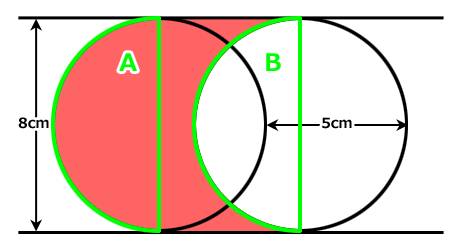
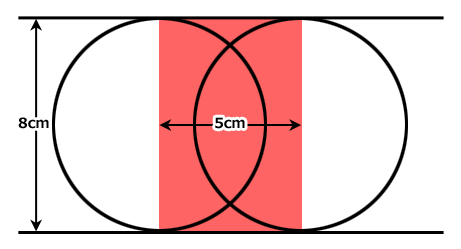
直径8cmの円が二つ、5cmほどずれて描かれています。
左の円は赤色、右の円は白色、円と円の間は赤色です。
赤い部分の面積はいくらでしょう？
しばらく考えてください。分かりましたか？
＋ 解答はここをクリック
説明します。
左の赤い円の左半分Aを、右の白い円の左半分Bに移動します。
移動すると赤い部分は長方形になりました。
もともと円と円の距離は5cmなので、円の中心と中心の距離も5cmになります。
よって赤い部分の面積は、8cm×5cm＝40c㎡になります。
重なっている部分の面積
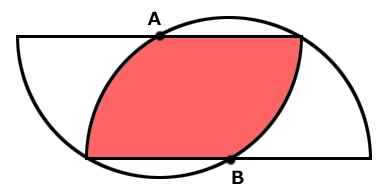
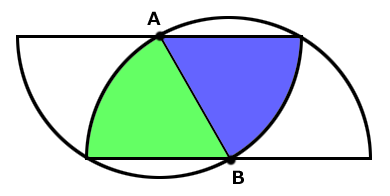
図のように半円同士が重なっています。
AとBは半円の円の中心であり、それぞれの円弧の1/3の位置です。
半円の半径は6cmです。
さて赤い部分の面積はいくらでしょう？
しばらく考えてください。分かりましたか？
＋ 解答はここをクリック
説明します。
難しく考えず、AとBを補助線で結びます。
角度60°の円弧が二つ出てきました。60°は360°の1/6です。
面積は、6cm×6cm×3.14÷6×2＝37.68c㎡になります。
もっと見る？
-
-
【まとめ】頭の体操★頭の固い人には溶けないかも！
解けそうで解けない問題を集めてみました。頭の良さより柔らかさが必要です。