<頭が固い人には解けない問題?>
扇形から円が、はみ出している図形
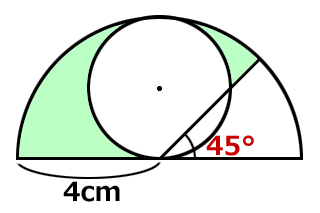
緑の部分の面積はいくらでしょう?
扇形から円が、はみ出しています。少しややこしそうです。
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
円の面積の公式は半径×半径×3.14です。
扇形の中心の角度は180-45で135度です。
緑の扇形の面積です。
4×4×3.14×135/360=18.84㎠
右下が欠けた中央の円の面積はいくらでしょう?
分かりやすいように補助線を青円の中心から縦横に入れてみます。
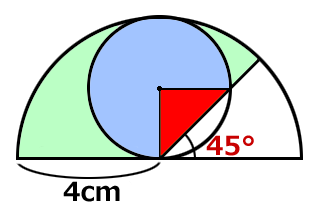
補助線を入れたら、とても分かりやすくなりました。
赤は頂点が90度の直角三角形、青は半径2cmの円です。青円の中心角は270度です。
青の面積はこちらです。-> 2×2×3.14×270/360=9.42㎠
赤の面積はこちらです。-> 2×2÷2=2㎠
緑の面積は「扇形ー青ー赤」です。
緑の面積は「18.84-9.42-2」で、7.42㎠です。
3個の正方形の面積
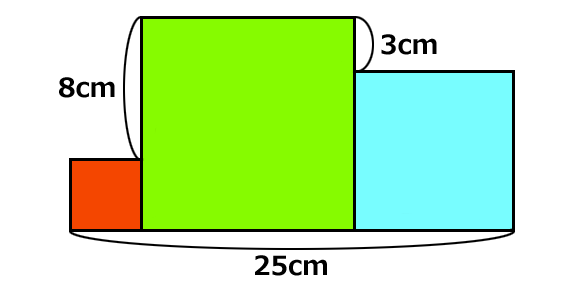
赤と緑と青の正方形があります。寸法が分かっているのは3箇所だけです。
さて3個の面積の合計はいくらでしょう。
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
では緑から赤と青を切り離してみましょう。
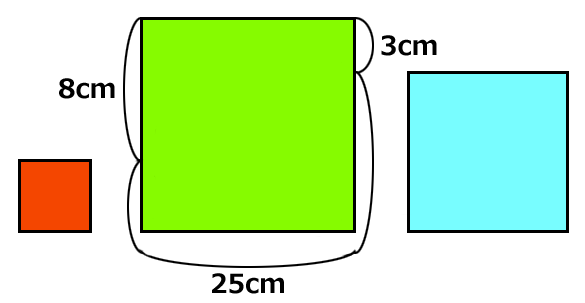
緑の一辺の長さが分かりましたか?
え?分からない?!
緑の一辺の長さは(8+25+3)÷ 3で12cmです。
なぜって?... なぜでもです。
赤の面積:(12-8)×(12-8)= 16
緑の面積:12×12=144
青の面積:(12-3)×(12-3)= 81
よって3個の面積の合計は、16+144+81で241㎠です。
円の中にある小さな正方形の面積
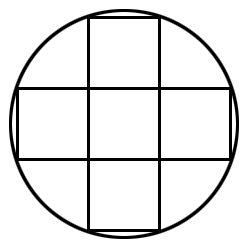
直径10cmの円の中に、同じ大きさの正方形が5個ほどピッタリと入っています。
この1個の正方形の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
では青い色の補助線を入れてみましょう。

青い補助線は正方形です。
そして赤い三角形と緑の三角系の面積も同じ面積です。
赤い三角形を切り取って緑の部分に移動しましょう。4個とも移動します。
十字形に並んでいた5個の正方形が、1個の大きな正方形になりました。
大きな正方形の面積は、円の直径が10cmですので、10×10÷2で50㎠です。
大きな正方形の面積は、小さい正方形5個分ですので、1個の面積は50÷5で10㎠です。
さいごに
難しい問題も補助線を入れると、急に分かりやすくなります。
面積の問題の多くは、補助線が命です。
頑張って難しい問題を解いていきましょう。
なんか難しい問題があるとワクワクしませんか?
もっと見る?
-

-
【まとめ】頭の体操★頭の固い人には溶けないかも!
解けそうで解けない問題を集めてみました。頭の良さより柔らかさが必要です。








