<三角形の面積はなぜ底辺×高さ÷2なのか?鈍角三角形は難しい>
三角形の種類
三角形は内角の大きさによって三種類に分けられます。
- 鋭角三角形(えいかくさんかっけい)
すべての角が90度より小さい三角形です。 - 直角三角形(ちょっかくさんかっけい)
90度ちょうどの角がある三角形を直角三角形といいます。 - 鈍角三角形(どんかくさんかっけい)
一つでも90度より大きな角があれば鈍角三角形です。
三角形の面積を求める式は以下のとおりです。
三角形の面積=底辺×高さ÷2
簡単ですね。でも鈍角三角形は説明できますか?
直角三角形
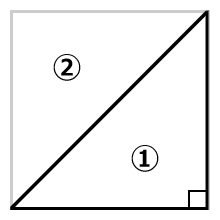
直角三角形は補助線を引いて四角形にするとわかりやすいですね。四隅は90度です。
底辺×高さ÷2で①の面積を求めることができます。
鋭角三角形
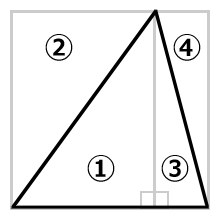
下図の様に補助線を引きます。
鋭角三角形は直角三角形が二つあると考えると分かりやいです。
鈍角三角形
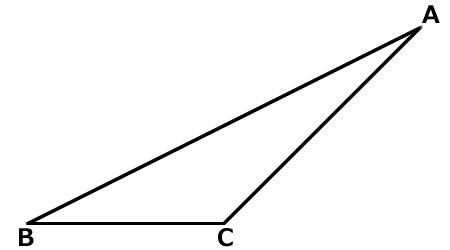
このような鈍角三角形の面積は「底辺×高さ÷2」で説明できるのでしょうか。
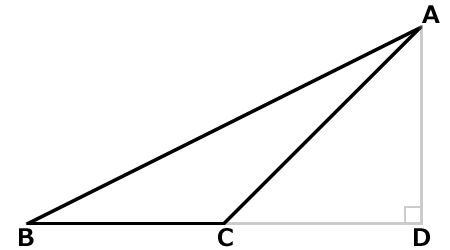
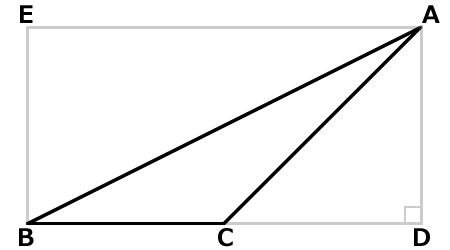
鈍角三角形ABCに補助線を追加して、直角三角形ABDを作成します。
「底辺×高さ÷2」の底辺はBD、高さはADになります。
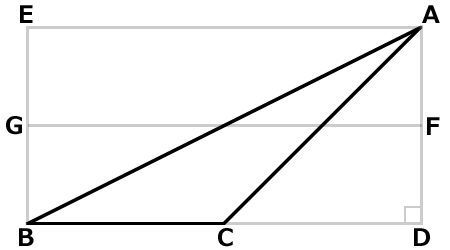
辺ADと辺BDと平行の補助線を引き、長方形AEBDを作成します。
長方形AEBDの中央に補助線GFを引きます。辺EGと辺GB、辺AFと辺FDは同じ長さです。
直角三角形ABDの面積は長方形FGBDと同じになります。(三角形の面積=底辺×高さ÷2)
直角三角形ABDから直角三角形ACDを取り除くと鈍角三角形ABCの面積になります。
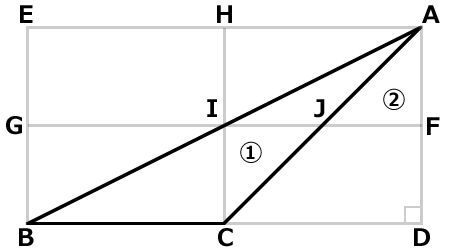
補助線HCを引きます。
三角形①と②の面積は同じです。
直角三角形AJFを180度回転させ、直角三角形JICにはめ込みます。(②を①にはめ込みます。)
直角三角形ACDと四角形FICDは同じ面積になります。
よって鈍角三角形ABCの面積は四角形IGBCの面積と同じになります。
四角形IGBCは底辺×高さ÷2となります。
まとめ
直角三角形ABDと四角形FGBDは同じ面積です。
直角三角形ACDと四角形FICDは同じ面積です。
鈍角三角形ABCの面積=直角三角形ABDの面積ー直角三角形ACDの面積とも言えます。
少しややこしかったですね。お疲れさまでした。
公式を使えば三角形の面積なんてすぐに計算できます。
三角形の面積=底辺×高さ÷2は、直角三角形と鋭角三角形は簡単にイメージできます。
でも鈍角三角形はイメージできませんでした。
他の面積の公式を使用して説明するのも、なんか違うような気がしました。
もっと分かりやすい説明があれば教えてください。
追加:「その2」の説明です。
追加 鈍角三角形その2
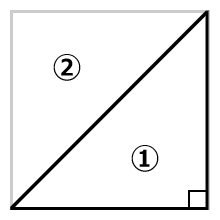
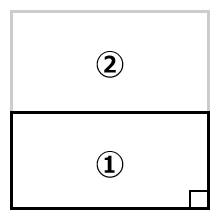
三角形の面積は、底辺×高さ÷2です。
①と②の面積は同じです。
底辺×高さ÷2は以下の様に書き換えることができます。
今回はこの考えを応用します。
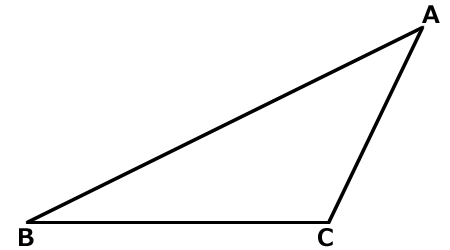
鈍角三角形ABCを用意します。
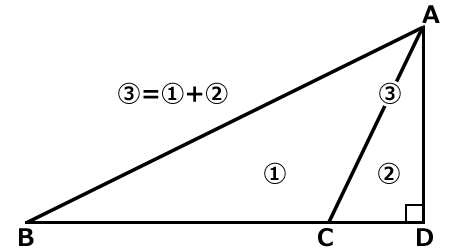
直角三角形ACDを追加します。
③は直角三角形ABDです。
面積は③=①+②です。
三角形③は大きな直角三角形ABDです。
三角形②は小さな直角三角形ACDです。
三角形①は面積を求める鈍角三角形ABCです。
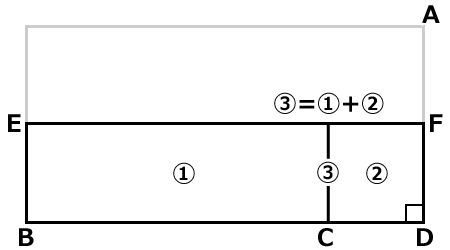
三角形を四角形に変換しました。
以下の図は三角形の面積と同じです。(辺AFと辺FDの長さは同じです。)
四角形①②③と三角形①②③の面積は同じです。
四角形①の面積は、四角形③ー②になります。
四角形①の面積は底辺×高さ÷2で、三角形の面積の式と同じです。
四角形①は、鈍角三角形ABCの面積となります。
こちらの説明の方が分かりやすいですか?
人からアドバイスをいただきました。
よかったら参考にしてください。