<頭が固い人には解けない問題?>
欠けている平行四辺形を二等分?
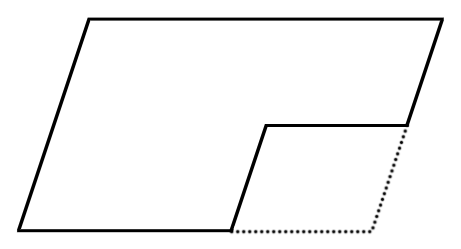
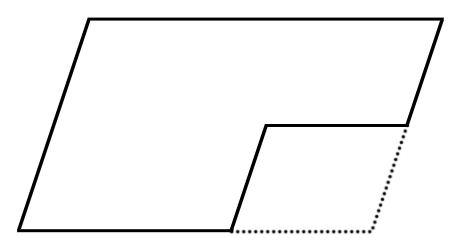
大きな平行四辺形の右下部分が、小さな平行四辺形で切り取られています。
一部を切り取られた平行四辺形を、1本の直線で二等分してください。
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
この問題の解答は三つあります。
解答1
平行四辺形を二等分する場合、どうすればいいのでしょう。
簡単です。対角線を1本引けばいいのです。
左上から引いても、右上から引いても、対角線で分けられた面積は同じです。
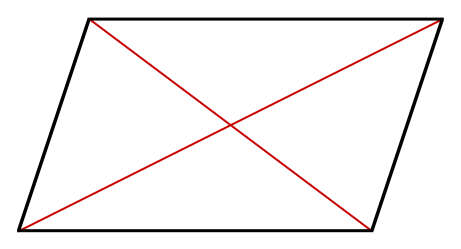
対角線を2本引きます。
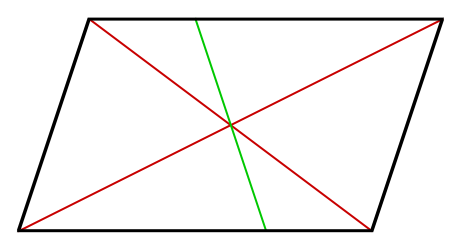
対角線の交点を通る直線を適当に引きます。
この適当に引いた緑の直線の左右の面積は同じです。
対角線の交点を通る直線で分けられた二つの面積は必ず同じになります。
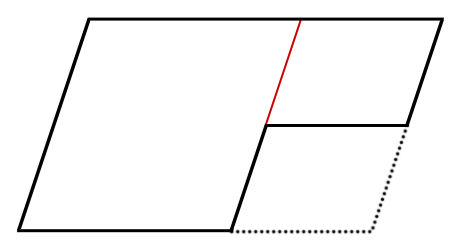
欠けた平行四辺形を二つに分けます。
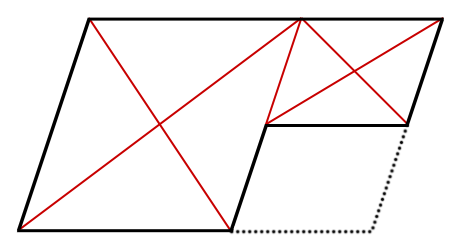
それぞれの平行四辺形に対角線を引き、交点を求めます。
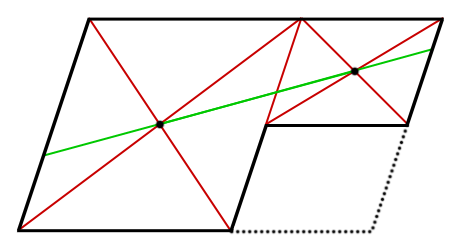
二つの交点を通る直線を引きます。
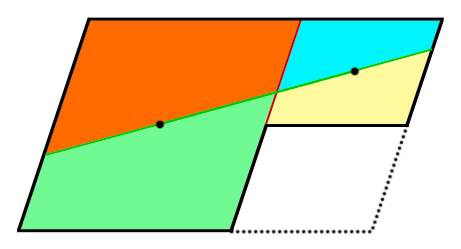
赤と緑、水色と黄色は同じ面積になります。
解答2
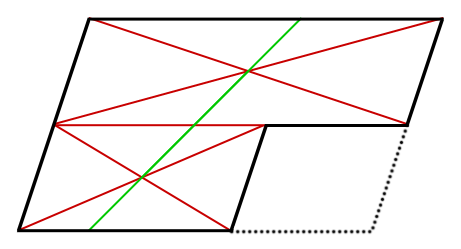
今度は平行四辺形を上下に分け、それぞれに交点を求めます。
二つの交点を通る直線を引きます。
緑の直線で分けられた二つの面積は同じになります。
解答3
今度は、欠けていない大きな平行四辺形から小さな平行四辺形を引くイメージです。
解答1と解答2が足し算なら、解答3は引き算のイメージです。
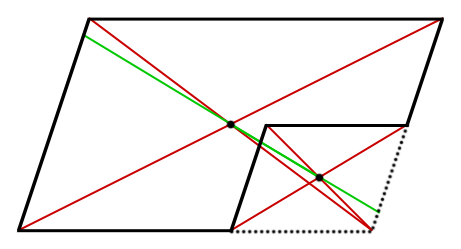
欠けていない大きな平行四辺形の交点と、欠けている小さな平行四辺形の交点を求めます。
二つの交点を通る直線を引きます。
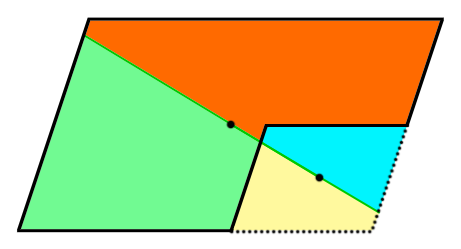
緑の直線で分けられた二つの面積は同じになります。
でも、なんかピンときませんね。
欠けていない大きな平行四辺形ですが「赤+水色」と「緑+黄色」は同じ面積です。
水色と黄色も同じ面積なので、赤=緑となります。
同じ長方形が3個
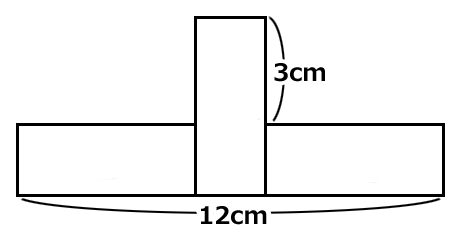
同じ長方形が3個あります。
1個の長方形の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
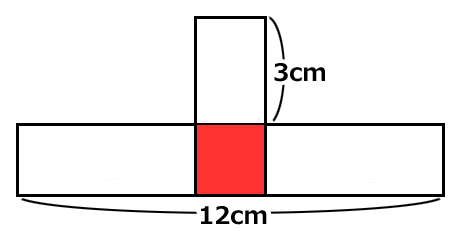
赤い部分ですが、同じ長方形ですので正方形になります。
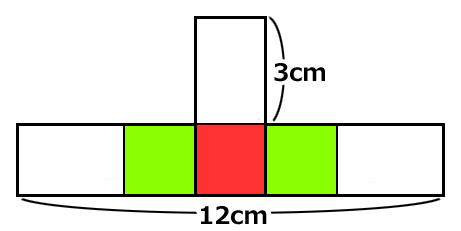
同じ大きさの正方形を左右に描きます。
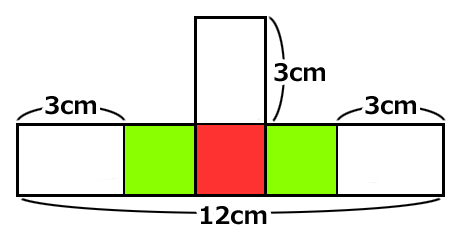
3個の長方形は同じなので、左右の長方形の白い部分の長さは3cmです。
正方形の寸法は(12-3×2)÷ 3=2cmとなり、長方形の短辺も2cmです。
長方形の長辺は3+2=5cmです。
よって長方形の面積は、2×5=10㎠になります。
長方形の中に円が3個?
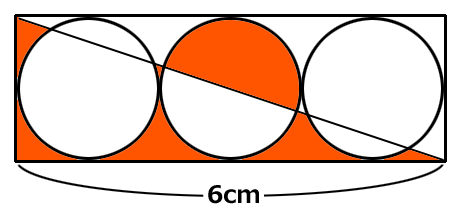
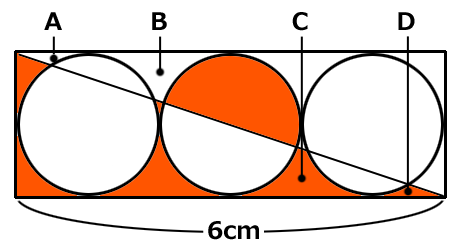
長さ6cmの長方形の中に、ピッタリ円が3個あります。
赤い部分の面積はいくらでしょう?
しばらく考えてください。分かりましたか?
+ 解答はここをクリック
長方形の縦は円の直径なので2cmです。
長方形の面積は2×6=12㎠になります。
円の面積は半径×半径×円周率なので、1×1×3.14=3.14㎠です。
赤い部分の面積は、長方形から円を3個引いてから2で割り、円の半分を足します。
長方形の面積は、2×6=12㎠です。
1個の円の面積は、1×1×3.14=3.14㎠です。
長方形から3個の円を引いて2で割り、半円を足します。
赤い部分の面積は(12-3.14×3)÷ 2 +(3.14×0.5)=2.86㎠です。
と、思っていたらこんな解答がありました。
AにDを、BにCを移動し、中央の円を半径が垂直になるよう回転させます。
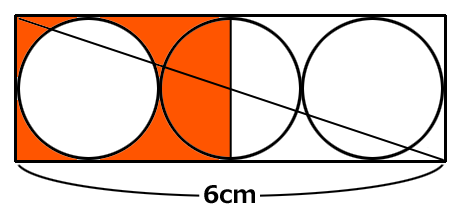
赤の面積は、2×3-1×1×3.14=2.86㎠です。
ずっとこっちのほうが簡単でした。
さいごに
シンプルな問題をわざわざ複雑にして解いていました。
練習問題を普段から頑張っていたら、すぐに気付いて解けていたはずです。
数をこなして、練習問題からヒントをたくさん得るようにしましょう。
もっと見る?
-

-
【まとめ】頭の体操★頭の固い人には溶けないかも!
解けそうで解けない問題を集めてみました。頭の良さより柔らかさが必要です。




















